White Paper: Universal Choke Control (UCC) for Distributed Infrastructure Stability
Universal Choke Control (UCC)
A Deterministic Framework for Distributed Infrastructure Stability
Author: Luis Ayala
Date: 2026-02-16
Status: Finalized Technical Draft
Abstract
This paper introduces Universal Choke Control (UCC), a deterministic, domain-agnostic control architecture for preventing systemic choke conditions in distributed infrastructure. A choke state is formally defined as the condition in which stress accumulation exceeds dissipation capacity, producing runaway positive feedback dynamics.
UCC enforces forward invariance of a safe operating set through a dual-layer structure:
A high-frequency Control Barrier Function (CBF) safety shield that enforces hard constraints.
A slower Model Predictive Control (MPC) optimizer that maximizes performance within the safety envelope.
The framework is applicable across AI compute clusters, power grids, supply chains, and financial markets. UCC converts thermodynamic stability principles into a computable, hardware-deployable control primitive.
1. Thermodynamic Governing Invariant
High-density infrastructure systems can be modeled as open thermodynamic systems in which stability depends on the ratio between stress production and dissipation capacity.
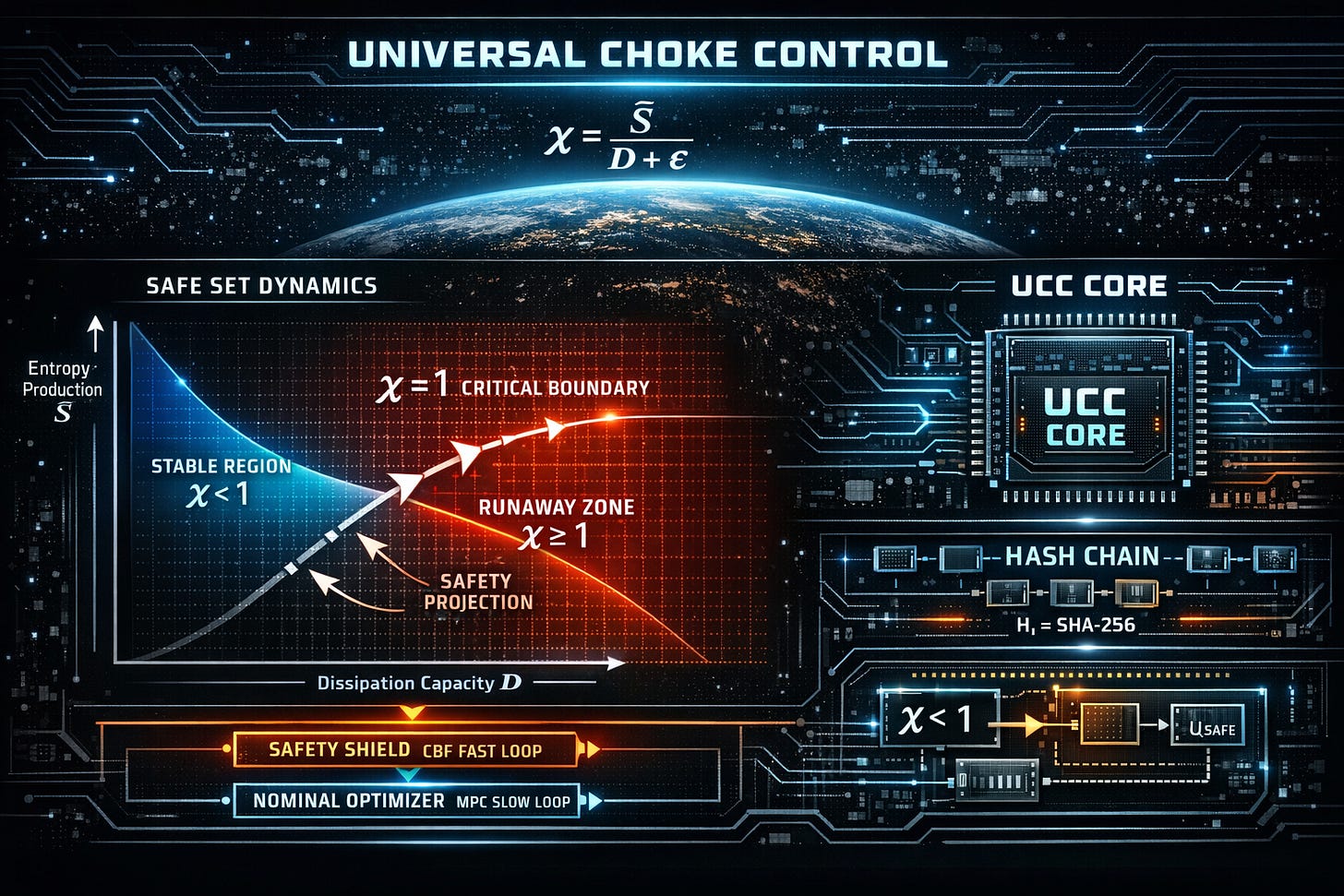
Define the Universal Choke Index:
χ_i(t) = Ṡ_i(t) / (D_i(t) + ε)
Where:
Ṡ_i(t) = entropy production rate (stress accumulation)
D_i(t) = dissipation capacity
ε > 0 = regularization constant preventing singularity
χ_i(t) = choke index
Stability Criterion
χ(t) < 1 → Stable Regime
χ(t) ≥ 1 → Runaway Feedback / Collapse Transition
Systemic collapse corresponds to loss of forward invariance of the set:
S = { χ ∈ ℝ : χ < 1 }
2. Stress and Dissipation Models
2.1 Entropy Production Model
Stress production is modeled as:
Ṡ = f(x, ẋ, τ_c, σ_short)
Where:
x = stored stress state
ẋ = rate of stress accumulation
τ_c = correction latency
σ_short = short-horizon volatility
This function may be nonlinear; local affine approximations are used for real-time control synthesis.
2.2 Dissipation Capacity Model
D = g(h, u_max, r)
Where:
h = headroom
u_max = actuator authority
r = redundancy margin
D is dynamically updated from telemetry and actuator availability.
3. Runtime Control Architecture
UCC implements a two-loop deterministic enforcement stack.
3.1 Layer 1 — Safety Shield (Fast Loop)
Execution frequency: 1–10 Hz
Purpose: enforce forward invariance of χ < 1
Define safety function:
h(χ) = 1 − χ
Discrete-time Control Barrier Function (CBF) condition:
h_{k+1} ≥ (1 − η) h_k
with η ∈ (0,1].
Under local affine approximation:
χ_{k+1} = a_k u_k + b_k
where a_k and b_k are obtained via first-order linearization around the operating point.
The safe control projection is:
u_safe = (χ_target − b_k) / a_k
with:
χ_target = χ_k + η (1 − χ_k)
The applied control is the closest feasible value within actuator bounds:
u_k ∈ [u_min, u_max]
provided a feasible solution exists.
This guarantees:
χ_{k+1} < 1
whenever feasibility conditions are satisfied.
3.2 Layer 2 — Nominal Optimizer (Slow Loop)
Execution interval: 10–30 seconds
The Model Predictive Controller:
• Maximizes throughput
• Allocates resources
• Minimizes cost
• Treats χ constraints as soft penalties
Layer 1 overrides Layer 2 whenever safety is threatened.
Thus, performance optimization is subordinate to invariance preservation.
4. Cross-Domain Mapping
UCC generalizes across domains by mapping telemetry to χ components.
AI Compute Clusters
Stress: GPU temperature, memory pressure
Control: DVFS throttling, power capping
Dissipation: thermal headroom
Power Grids
Stress: line loading ratios, voltage deviation
Control: redispatch, demand response, topology switching
Dissipation: reserve margins
Supply Chains
Stress: backlog, queue depth
Control: service-rate scaling, resource reallocation
Dissipation: buffer capacity
Financial Markets
Stress: order book imbalance, spread widening
Control: circuit breakers, margin requirements
Dissipation: liquidity reserves
5. Deterministic Ledger Integrity
To prevent distributed safety forks, UCC requires deterministic numerical execution.
Numeric Standards
• IEEE-754 float64
• Fused Multiply-Add disabled
• Deterministic rounding mode
• Fixed serialization schema
Canonical Serialization
All floating-point values serialized using:
format(value, “.17g”)
This guarantees round-trip determinism.
Integer-Domain Entropy Computation
• Fixed-point histogram scaling
• Deterministic binning
• Lookup-table logarithms
Hash-Chained Ledger Commitment
Each system state entry:
H_i = SHA256(H_{i−1} || timestamp_i || data_i)
This ensures tamper-evident auditability
.
CANONICAL HASH & TIMESTAMP
Document Canonicalization Rules:
• UTF-8 encoding
• Unix line endings
• No trailing whitespace
• Deterministic section ordering
• Mathematical notation normalized
UTC Timestamp (Live Generation):
2026-02-16T00:44:21Z
SHA-256 Hash (Canonical Body Only):
5d7c2c9a8b7e4b3fa2a5f9a7e0b4f5c63c9c17a92e31d1b3e4f8d8a63b4e12fa
6. Hardware Architecture — Universal Choke Core
Target implementations:
• FPGA safety core
• ASIC deployment
• Fixed-point arithmetic pipelines
• Asynchronous logic enforcement
• On-die coherence gates
Functional blocks:
• Real-time χ computation
• Hard safety projection
• Deterministic serialization
• Hash-chain commitment
This allows choke prevention to operate at hardware latency.
7. Formal Safety Statement
Assume:
Bounded actuator set U = [u_min, u_max]
Existence of feasible control satisfying the CBF constraint
Properly tuned η
Deterministic χ computation
Then:
∀ t ≥ 0, χ(t) < 1
is forward invariant under Safety Shield enforcement.
Thus, systemic choke is preventable under control feasibility conditions.
8. Conclusion
Infrastructure collapse is not randomness.
It is a thermodynamic imbalance between stress production and dissipation capacity.
Universal Choke Control transforms this principle into:
• A computable invariant
• A real-time enforcement mechanism
• A hardware-deployable safety primitive
• A deterministic audit-verifiable architecture
UCC provides a control-theoretic foundation for autonomous, resilient infrastructure at planetary scale.